Background information and purpose of the experiment:
In the process of enamelling of small household appliances, one of the most important parameters is the humidity of the compressed air that transports the enamel powder to the enamel guns. It plays a key role in ensuring the stability of powder transport and the quality of the future coating. Air that is too dry can lead to excessive dusting and adhesion problems, and can also generate excessive electrostatic charges. Conversely, too high humidity can cause powder caking in feeders or nozzles, lower electrostatic charges, and thus lead to unstable application and surface defects.
A relatively simple compressed air treatment device—a dehumidifier—is responsible for regulating the humidity level. The desired powder moisture level at the device output depends on the ambient temperature and humidity, as well as the input parameters of the enamel powder.
The goal of the study is to understand how to control the device to obtain the desired powder moisture level at the output, depending on the needs.
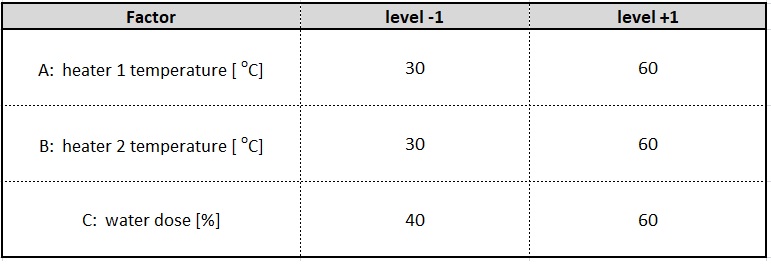
For this purpose, three factors were tested at two levels using a full-factorial experiment. The tested factors and their levels are shown in the Table and Diagram below. The response from the experiment will be the powder moisture measured at the device outlet.
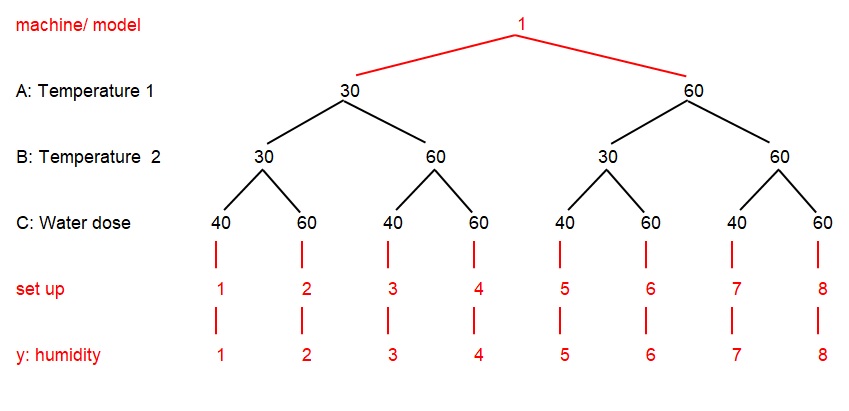
To test all combinations of these 3 factors on 2 levels (each with each) we need 8 runs of the experiment, as shown in the diagram below.
So the experiment we will perform is a full factorial design: 2^3=8 , where:
- 2 is the number of testing levels
- 3 is the number of factors
- 8 is the number of runs
Numerical analysis of a full factorial design:
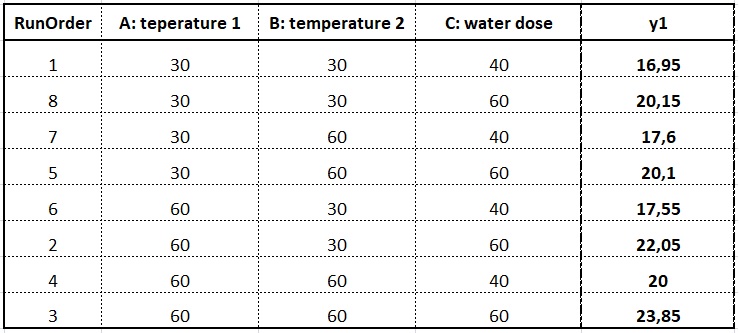
The experiment was carried out in a fully randomized manner according to the 2^3=8 full factorial experiment matrix shown below and the following results of powder moisture at the machine outlet were obtained.
The number of effects we can estimate in a given doe is always 1 less than the number of runs, meaning in our case we can esimate 7 different effects independently. A 2^3=8 experiment is said to have 7 degrees of freedom (dF). These are:
- 3 dF are the main effects: A, B, and C
- 3 dF are the second-order interaction effects: A*B, A*C, and B*C
- 1 dF is the third-order interaction effect: A*B*C
Calculating the above effects is possible because the doe matrix is balanced and orthogonal.
Balanced testing means that each factor is tested an equal number of times at each level. In the case of a 2^3=8 experiment, each factor is tested four times at its -1 level and four times at its +1 level. We’ll get to orthogonality in a moment.
Estimating main effects sizes
The main effect of a factor shows how the average y (response from doe, in our case y: powder moisture) changes when this factor changes from level -1 to level +1. To estimate it, find the mean y for all runs in which the given factor was at +1, then find the mean y for all runs in which the given factor was at -1. The difference in these means is a measure of the effect of the given factor.
A positive effect means that changing the factor level from -1 to +1 causes an increase in the mean y, while a negative effect means a decrease.
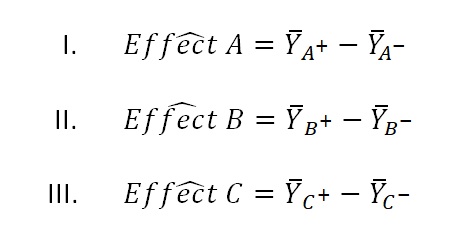
Using the DOE matrix below, let’s calculate Effect A, which in our case is: How the average moisture content of the powder changes when I increase temperature 1 from 30oC to 60oC.


Interpretation of Main Effect A
Increasing the temperature of heater 1 from 30 to 60°C causes an increase in mean humidity by 2.17%.
We calculate the remaining main effects in a similar manner. The summary results will be presented below.
Now we can move on to the second feature of the experimental matrix that allows us to perform the above calculations – orthogonality.
Orthogonality means that when I calculate the mean humidity when factor A is at +1, the influence of the other factors on this mean is nullified, since each of them is within the mean by 2x at -1 and 2x at +1. Therefore, even if factors B and C had an influence on the mean humidity, within the mean their influence on this mean is neutralized. A similar situation occurs when I calculate the mean humidity when factor A is at -1. Of course, orthogonality also applies to other factors and their interactions.
Calculating the size of interaction effects
A second-order interaction, e.g., A*B, means that the effect of changing factor A from -1 to +1 will be different depending on the setting of factor B. “Different” could mean the opposite effect, a much smaller effect, or no effect at all. In our case, the AB interaction would mean that the effect of changing temperature 1 will produce a different effect on powder moisture content depending on the setting of temperature 2.
Interactions, especially second-order interactions, occur very frequently, and the inability to study them is the cause of most chronic problems. Only DoE, as an experimental method, allows us to understand the interactions.
The magnitude of the interaction effect is calculated analogously to the main effect:

The difference is that before we can calculate interaction effects, we need to determine the sign of a given interaction in a given run. To do this, we multiply the appropriate columns of the original experimental matrix together, as shown in the table below.

For example, in Run 1, to find the sign of the A*B interaction, we multiply the signs of factors A and B, i.e., -1 x -1 = 1, and that’s the sign the interaction takes.
The columns showing the sign of a given interaction are also balanced and orthogonal, allowing us to calculate the effects of the remaining degrees of freedom.
Let’s calculate the effect of the AB interaction:

We calculate the effects of the remaining interactions in a similar manner.
The table below shows the correct results of the remaining calculations.

Unlike main effects, the magnitude of an interaction effect doesn’t tell us how it works. To interpret an interaction effect, we need to graph it.
Next steps of this analysis in an article below!
Have questions, thoughts, or something that particularly piques your interest? Join the discussion below on our LinkedIn post. Follow us to stay up to date.