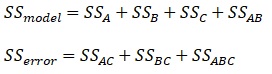Poniżej znajdziesz wcześniejsze części tego artykułu:
Jak zweryfikować jakość modelu?
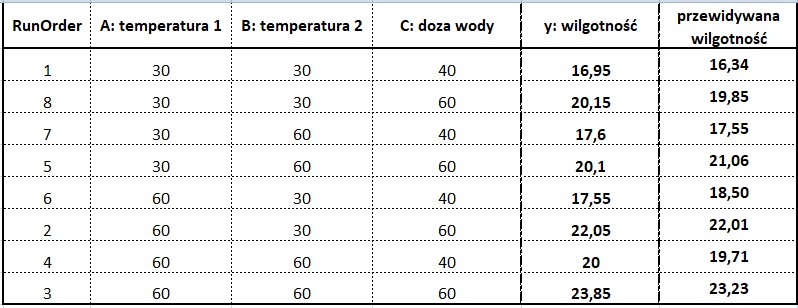
Jak zweryfikować na ile trafnie przewiduje on wilgotność dla różnych ustawień czynników A, B i C oraz interakcji AB? Najlepiej skonfrontować wilgotność przewidywaną przez równanie predykcyjne z wynikami które znamy z doe, czyli z y, który otrzymaliśmy w kolejnych przebiegach eksperymentu. Tabela poniżej zawiera y otrzymany z doe oraz ten przewidziany przez model dla wszystkich 8 przebiegów eksperymentu.
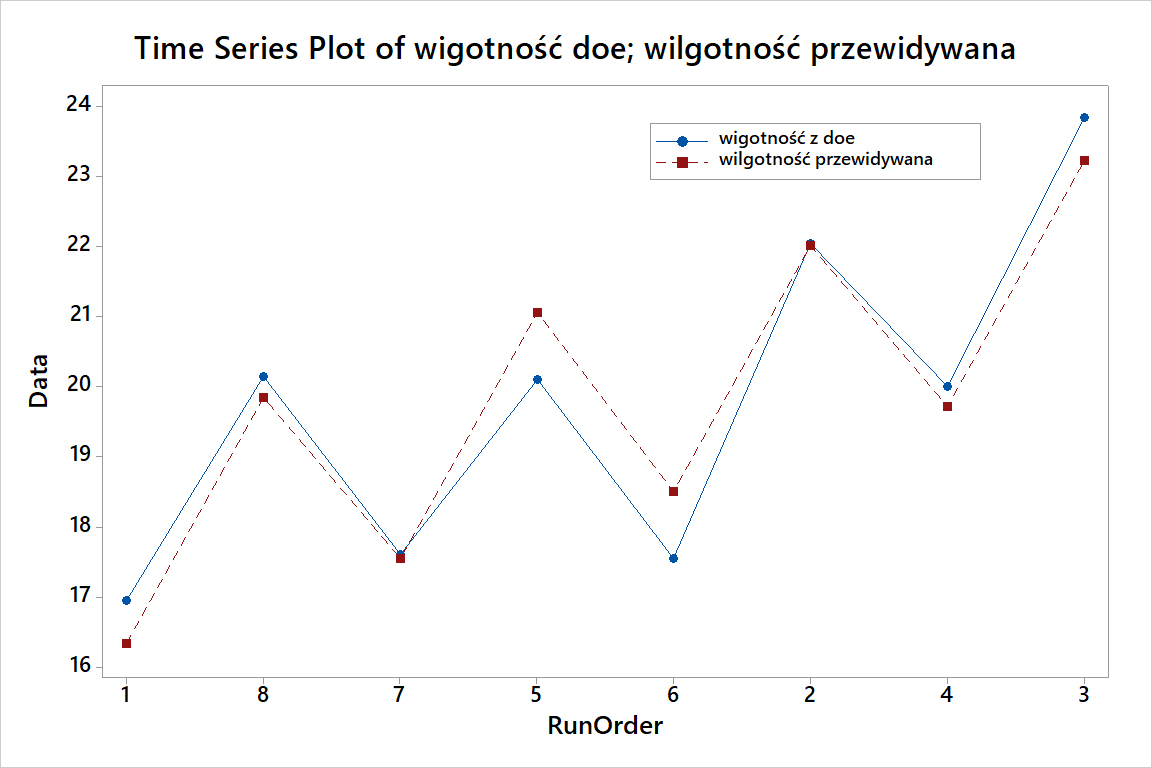
Różnice na ile wyniki uzyskiwane przez równanie predykcyjnie są inne od tych uzyskanych w doe można przedstawić graficznie jak to pokazano na wykresie poniżej.
Kliknij, aby powiększyć
Im większe różnice między zmiennością zmierzoną podczas doe a tą przewidzianą przez równanie predykcyjne tym model słabszy. Innymi słowy niewielkie różnice pomiędzy tymi dwoma liniami oznaczają, że za pomocą równania, w którym umieściliśmy 4 z 7 efektów, możemy wyjaśnić większość zmienności jaką wykreowaliśmy w tym doe.
Jakość modelu możemy również ocenić ilościowo, za pomocą tzw. współczynnika determinacji R2. Pokazuje on jaką część zmienności wykreowanej w tym doe, wykreowały efekty uwzględnione w modelu.
Wysoki R2 oznacza, że efekty uznane za istotne wyjaśniają większość zmienności, niski R2 oznacza, że mamy dużo niewyjaśnionej zmienności (wysoki poziom zakłóceń).
Jak obliczyć R2?
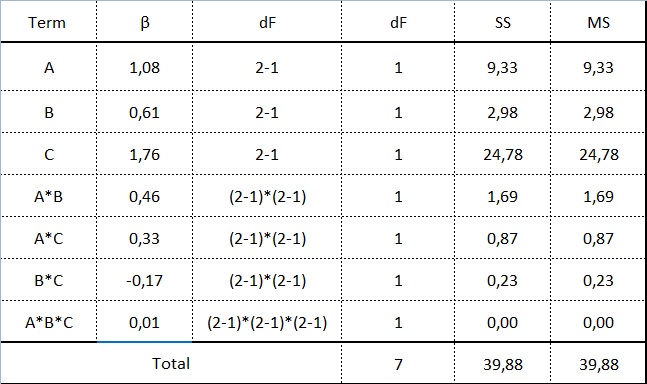
W eksperymencie 23=8 zmienność potencjalnie kreowały 3 efekty główne A, B i C oraz 4 efekty interakcji: AB, AC, BC i ABC. Aby zrozumieć ich wpływ na y: wilgotność proszku, możemy zrobić dwie rzeczy:
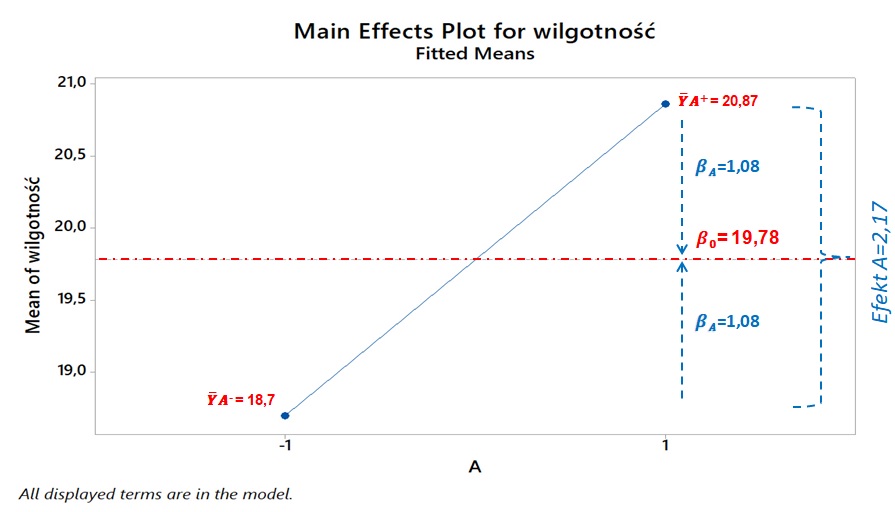
- Obliczyć wielkości efektów, czyli jak zmiana danego efektu z poziomu -1 na +1 wpływa na średni y (tak jak to pokazano w części 1)
- Oszacować, ile ze zmienności w doe wykreował każdy z nich.
Weźmy dla przykładu efekt główny A. Żeby zrozumieć wpływ A na y możemy:
Kliknij, aby powiększyć
Wyniki obliczeń dla wszystkich efektów w tym doe pokazuje tabela poniżej:
Kliknij, aby powiększyć
Nasze równanie predykcyjne zbudowaliśmy z użyciem A, B i C oraz interakcji AB, uznając pozostałe efekty, czyli pozostałe interakcje, za nie istotne (niekreujące zmienności w tym DOE).
Dokonując obliczeń z wykorzystaniem wyników zamieszczonych w tabeli powyżej:
W naszym przykładzie R2 wynosi 97%. Oznacza to, że za pomocą czynników A, B, C oraz interakcji AB możemy wytłumaczyć 97% zmienności wykreowanej w tym doe.
Im wyższy R2 tym lepiej? Co zrobić, żeby poprawić niezadowalający nas R2? Możemy dorzucić nieistotne efekty do modelu zawyżając R2. Gdybyśmy wrzucili wszystkie 7 efektów R2 wyniosłoby 100%.
Dlaczego jednak nie powinniśmy tego robić? Bo to nie ma sensu! Jeżeli dany czynnik uznajemy za nieistotny, jeżeli nie wykreował zmienności to tylko zaśmieci model. Jego działanie w tym doe uznajemy za zakłócenie. Jeżeli jest to czynnik, o który wierzymy, że ma istotny wpływ na y, przetestujmy go w kolejnym doe na zmienionych poziomach testowania, natomiast jego obecność w aktualnym równaniu nie ma zasadności, ponieważ nie wykreował on zmienności.
Jako sprawdzenie czy nasze równanie nie zostało zanieczyszczone nieistotnymi efektami mamy skorygowany współczynnik determinacji R2-adjusted. Uwzględnia on nie tylko SS dla poszczególnych składników zmienności, ale koryguje o ilość stopni swobody.
Jak obliczyć R2 – adjusted?
Podsumowując, kiedy model zawiera A, B, C i AB:
R2 = 97%, R2adj = 94%
Kiedy różnica między R2 a R2adj jest duża, oznacza to, że w modelu znajduje nieistotny efekt. W naszym przypadku ta różnica jest niewielka, co oznacza, że model nie jest zaśmiecony.
Jak wrzucenie nieistotnego efektu do równania wpływa na R2 i R2 adjusted?
Najłatwiej będzie to sprawdzić dodając nieistotny czynnik do naszego równania. Zepsujmy model dodając do niego interakcję B*C, dla której SSBC = 0,23 (tabela powyżej)
Porównanie
Model zawierający: A, B, C, AB :R2=97%, R2adj =94%
Model zawierający: A, B, C, AB, BC :R2=98%, R2adj =92%
Dodanie BC nieco zwiększyło R2. Ta niewielka różnica wynika z tego, że efekt BC jest bardzo mały.
R2adj spadło, dzięki temu, że mimo niewielkiego spadku SSerror straciliśmy 1 dF w mianowniku (3 na 2). Zysk w dopasowaniu był zbyt mały w stosunku do utraty tego dF. W ten sposób R2adj – karze za nieistotne efekty w modelu.
Pytania:
- Czy równanie zawsze działa?
- Od czego zależy czy działa?