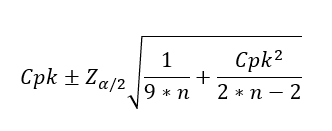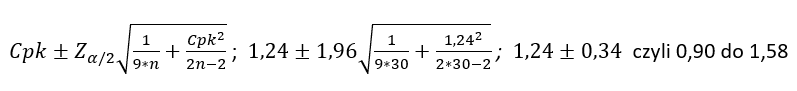Karty zachowania się procesu oraz histogramy z naniesionymi granicami specyfikacji pozwalają porównać głos procesu z głosem klienta. Podsumowania liczbowe, tak nazwać należy wskaźniki zdolności procesu, uzupełniają te porównania graficzne, ale nie są w stanie ich zastąpić. Głównym problemem podsumowań liczbowych nie są obliczenia, lecz ich prawidłowa interpretacja. Kluczem do używania jakiejkolwiek wskaźnika jest zrozumienie jego ograniczeń.
Jak często widziałeś raporty zawierające takie stwierdzenie Cpk procesu wynosi – i tu pada liczba (np.: 1,24)? Jakie pytania powinieneś zadać zanim zaczniesz wyciągać jakkolwiek wnioski?
- Czy system pomiarowy który dostarczył danych użytych do obliczeń został zweryfikowany i jest wystarczająco precyzyjny? (czy przeprowadzono MSA i czy zrobiono to prawidłowo?
- Jak dane zostały zebrane? Czy pochodzą z racjonalnego planu próbkowania, dzięki któremu odzwierciedlają źródła zmienności powodujące obecne na co dzień w tym procesie?
- Czy proces jest stabilny? Czy mamy tylko zmienność naturalną. Pamiętaj najpierw stabilność potem zdolność.
- Czy specyfikacje są rzetelnie zdefiniowane?
- Czy dane mają rozkład normalny?
- Ile danych użyto do obliczenia wskaźników zmienności?
Zakładając pozytywną odpowiedź na pytania 1 do 5, zatrzymajmy się nad pytaniem 6.
Cpk = 1,24, w większości przypadków takie stwierdzenie jest oparte na danych z próby/ sample, pobranej z dużo większej populacji. Zmienność istnieje! – oznacza to, że gdybyśmy z tego samego procesu, w ten sam sposób zebrali dane kolejny raz i obliczylibyśmy wskaźnik Cpk ponownie – najprawdopodobniej jego wartość byłaby inna niż 1,24.
Gdy raportujemy Cpk = 1,24, odbiorca może założyć, że jest to rzeczywista wartość Cpk a to nie prawda. 1,24 to jedynie estymacja (szacowana wartość). Lepszym sposobem raportowania byłoby stwierdzenie: „Nie znam prawdziwej wartości Cpk, ale na podstawie próby o liczności n = 30 jestem w 95% pewien, że mieści się ona w przedziale od 0,90 do 1,58.”
Statystyki są jedynie estymacją prawdy, a co za tym idzie, są obarczone błędem. To jak duży jest błąd wskaźnika zależy od:
- ilości danych / sample size, z której statystyka została obliczona
- poziomu ufności / confidence level, jaki chcemy przypisać danej statystyce.
Poziom ufności, np. 95% oznacza, że jeżeli wielokrotnie pobieram próbę z tego samego procesu w ten sam sposób i za każdym razem wyznaczam nowy przedział ufności 95%, to w 95% przypadków ten nowo wyznaczony przedział zawiera prawdziwą wartość wskaźnika – 5% nie.
Jeżeli weźmiemy pod uwagę, że zły poziom Cpk to wartość poniżej 1,00, a bardzo dobry to wartość powyżej 1,33, to przedział od 0,90 do 1,58 jest w praktyce bezwartościowy informacyjnie. Gdzie leży problem? Próba jest zbyt mała, albo inaczej – ilość danych użytych do obliczenia Cpk jest zbyt mała.
Jak obliczyć przedział ufności dla Cpk?
gdzie:
Cpk – to aktualna estymacja wskaźnika
n – ilość danych użyta do obliczeń,
Zα/2 – stała dla wybranego przedziału ufności. To wartość, dla której pole pod krzywą Gaussa po jednej stronie wynosi α/2. Aby ją wyznaczyć, przykładowo, dla poziomu ufności 95% należy:
- znaleźć α; 95% = 0,95 zatem α=1-0,95 =0,05
- znaleźć α/2= 0,05/2; α/2= 0,025
- znaleźć 1- α/2, 1- α/2= 1-0,025 =0,975
- znaleźć Z α/2 dla 1- α/2 w tablicach rozkładu normalnego. W tablicach znajdujemy pole o wartości 0,975 i odczytujemy Z, u nas ta wartość wynosi 1.96
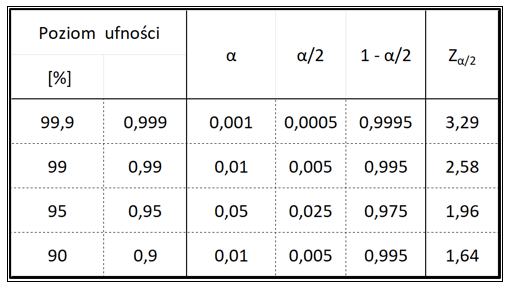
Tabela 1 przedstawia wartości Zα/2 dla najczęściej stosowanych przedziałów ufności.
Tabela 1
Wracając do naszego przykładu:
- Cpk = 1,24
- n =30
- Zα/2 =1,96
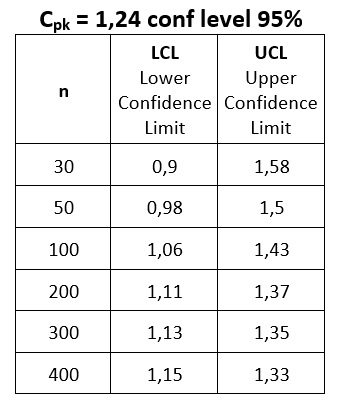
Ilu danych potrzebujemy? Policzmy jak będzie się zmieniał przedział ufności Cpk 1,24 dla różnych wielkości podgrup. Tabela 2 poniżej pokazuje wyniki obliczeń:
Tabela 2
Jeżeli chcemy pewność, że Cpk nie spadnie poniżej 1 potrzebujemy co najmniej 100 obserwacji. W zależności od pewności jakiej potrzebujemy powinniśmy definiować Dolny Limit Przedziału Ufności (Lower Confidence Limit) a nie tylko pożądaną wartość Cpk. Modyfikując zdanie początkowe: „Nie znam prawdziwej wartości Cpk, ale na podstawie próby o liczności n = 30 jestem w 95% pewien, że nie będzie mniejsza od 0,90”.
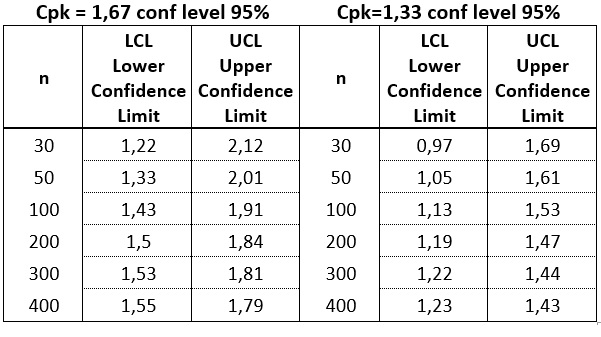
Im większa ilość danych tym przedział ufności węższy. W ogólnym obiegu istnieją dwa standardy co do pożądanego poziomu Cpk: 1,67 dla charakterystyk uznawanych za krytyczne i 1,33 dla pozostałych. Zobaczmy, jak kształtują się poziomy LCL dla obu tych wartości w zależności od ilości danych użytych do ich obliczenia.
Tabela 3
Ile zatem potrzebujemy danych do obliczania wskaźników zdolności? W większości praktycznych zastosowań Cpk nie interesuje nas, jak bardzo jest on wysoki, lecz czy nie spada poniżej pewnej wartości granicznej. W takich przypadkach powinniśmy interesować się jaki jest Lower Confidece Limit, a nie jaka jest wartość aktualnie policzonego wskaźnika.
Ilość danych użytych obliczeń jest istotnym ograniczeniem wskaźników zdolności. Czy to znaczy, że ten wskaźnik jest zły – nie. Każda metoda statyczna, każdy wskaźnik je ma. Dopiero ich poznanie pozwala używać ich tak żeby wnioski przyniosły nam realne korzyści.
Excel który oblicza poziomy LCL I UCL, dla zadanego poziomu ufności, wielkości próby i aktualnie oszacowanego poziomu Cpk do Waszej dyspozycji.
Żródło:
Donald J. Wheeler, Beyond Capability Confusion, 2nd edition, SPC Press
Mark L. Crossley, Size Matters, How good is your Cpk, really?,Quality Digest Magazine, 2000.1