Część pierwszą artykułu, w której której ustaliliśmy cele eksperymentu, wybraliśmy czynniki oraz poziomy ich testowania, znajdziesz tutaj
Co będziemy mierzyć podczas DOE?
1. Y lub najlepiej Yki główne, czyli metryki liczbowe opisujące efekt testowanych czynników.
Potrzebujemy zatem zmierzyć jakość żółtka oraz łatwość obierania. W tym momencie oceniamy to jedynie wizualnie, co najwyżej komentując efekty gotowania. W doe potrzebujemy danych ciągłych. Jeżeli wszystko co wiemy po przeprowadzeniu testu, to czy jajko jest dobre czy nie, to analiza będzie praktycznie niemożliwa. Jeżeli aktualnie w naszym procesie mamy np. tylko ocenę wizualną, to na potrzeby doe musimy znaleźć metrykę liczbową. Jest na kilka sposobów, ale o tym innym razem.
Jak poradzimy sobie w tym doe? Do oceny koloru użyjemy aplikacji Adobe Capture. Dzieki niej dla każdego jajka (po przekrojeniu) uzyskamy odczyt koloru w addytywnym modelu barw RGB (Reed Green Blue) stąd:
Y1 – Złocistość żółtka [Reed/Green]. Stosunek R/G jest wskaźnikiem przesunięcia barwy w stronę ciepła. Kiedy R jest zbliżony do G mamy neutralny żółty kolor, Kiedy R<G kolor przesuwa się w kierunku zielonego, czyli mniej apetyczne żółtko, im R > G kolor robi się cieplejszy, bardziej złoty, czasem lekko pomarańczowy.
Y2 – Zielony pierścień – wartość kanału G świadczy o przegrzaniu jajka, Im wyższy poziom G tym jajko wygląda mniej apetycznie
Kolejnym Y będzie skala porównawcza
Y3 – Jakość żółtka wizualnie – skala, która powstanie po doe, dzięki uporządkowaniu jajek od wizualnie „najładniejszego” do wizualnie „najbardziej przegrzanego” żółtka. Kolejnym jajkom nadamy numery, które będą analizowane jako wynik z doe. Im wyższy numer otrzyma jajko tym gorsze żółtko.
Do oceny jakości obierania użyjemy pomiaru czasu, za pomocą stopera z rozdzielczością 0,01 s zmierzymy:
Y4 – Czas obierania [s]. Teoretycznie im krótszy tym lepszy, chociaż niekoniecznie.
W związku z tym w naszym doe użyjemy wagi jubilerskiej z rozdzielczością 0,01g do pomiaru kolejnego Y:
Y5 – Masa skorupki [g]. Zwiększona masa skorupki będzie oznaczać, że nie oddzielała się ona „łatwo” od białka i część białka mogła „pójść ze skorupką”
2. Pozostałe Yki, na które mogą mieć wpływ testowane czynniki. Idea jest prosta, nie sztuka poprawić jeden Y a zepsuć te które np. teraz są dobre.
Y6 – Strata masy po ugotowaniu [%]. Liczona jako stosunek masy przed do po ugotowaniu. Teoretycznie masa nie powinna się zmieniać, ponieważ jajko zmienia jedynie stan skupienia, nie zmieniając objętości. W praktyce, para wodna ucieka przez pory w skorupce, część białka może się nieco odwodnić. Dla jajka, które nie pęknie (sytuacja pożądana) masa spada o około 0,5 do 2%, jeżeli pęknie straty będą duże większe. Ten Y nie ocenia wprost jakości żółtka czy łatwości obierania jajka, ale będzie wskaźnikiem jakości procesu gotowania.
3. Pozostałe pomiary:
W zależności sytuacji, możemy potrzebować zweryfikować poprawność ustawienia niektórych testowanych czynników. Jest to konieczne w sytuacji, gdy testowany czynnik ma pewną bezwładność (przykładowo studzenie i grzanie formy np.: odlewniczej czy w procesie wtrysku). Dodatkowo możemy chcieć zmierzyć poziom niektórych zakłóceń podczas doe, co być może przydać się podczas analizy.
Jaki projekt eksperymentu wybrać? Eksperyment pełno-czynnikowy czy ułamkowy?
Żeby przetestować 6 czynników na dwóch poziomach, mamy kilka możliwości:
- 26 = 64 – czyli eksperyment pełno-czynnikowy, gdzie 2 to ilość poziomów, 6 to ilość czynników a 64 ilość przebiegów
oraz trzy opcje eksperymentu ułamkowego:
- 26-3III=8
- 26-2IV=16
- 26-1VI=32
gdzie 2 to ilość poziomów, 6 to ilość czynników, -1,-2,-3 to ułamek, III, IV, VI to rozdzielczość eksperymentu, 8, 16, 32 to ilości przebiegów w zależności od wielkości ułamka.
Wyboru dokonujemy biorąc pod uwagę ilość przebiegów oraz jeżeli myślmy o eksperymencie ułamkowym koniecznie musimy wziąć pod uwagę rozdzielczość eksperymentu.
W przypadku 6 czynników zasoby potrzebne do zrealizowania eksperymentu pełno czynnikowego są za duże. W związku tym zdecydowaliśmy się na eksperyment ułamkowy. Scenariusz 26-3III=8, odrzucamy ze względu na rezolucje III, która jest obarczona wysokim poziomem uwikłań. 26-1VI=32, to ciągle za duże zasoby. Z trzech dostępnych opcji wybraliśmy ostatecznie 26-2IV=16, która jest dobrym kompromisem między ilością przebiegów a poziomem uwikłań.
O eksperymentach ułamkowych, uwikłaniach i rezolucji napiszemy innym razem.
Kreowanie matrycy eksperymentu:
Po wybraniu projektu eksperymentu, najlepiej przy pomocy oprogramowania (np.: Minitab, JMP i wiele innych) wykreuj matrycę eksperymentu, w naszym przypadku to matryca 26-2IV=16.
Oczywiście można to zrobić ręcznie. W przypadku eksperymentu pełnoczynnnikowego sprawa jest prosta. Jeżeli chodzi o eksperymenty ułamkowe, nieco bardziej skomplikowana i obarczona dużym prawdopodobieństwem pomyłki – ale nie jest niemożliwaJ. Wytłumaczymy, jak to zrobić, ale temat na całkiem inną opexową historię.
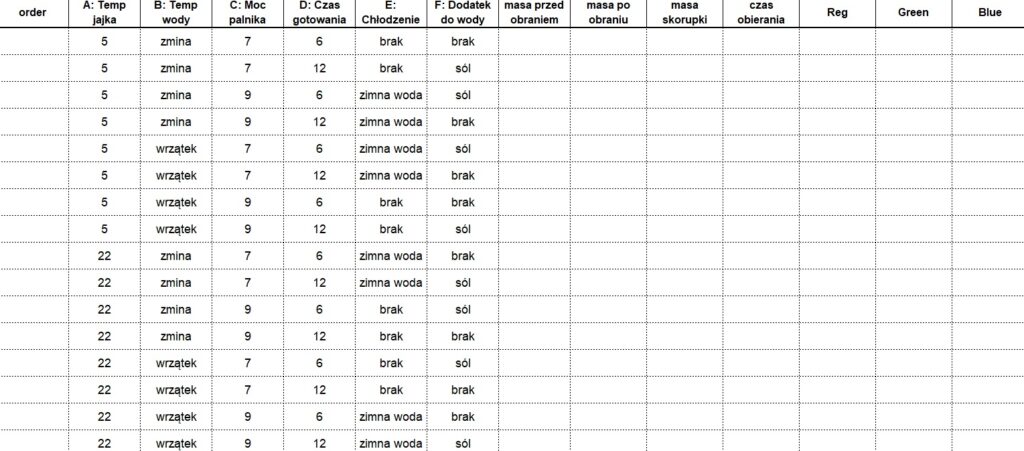
Matrycę eksperymentu do naszego przykładu przedstawia tabela poniżej.
Kliknij, aby powiększyć
Jeżeli planujesz wykonać eksperyment ułamkowy, zachowaj Strukturę Uwikłań. Będzie ona potrzebna do prawidłowej analizy eksperymentu.
Struktura Uwikłań w przypadku doe 26-2IV=16 wygląda następująco:
A + BCE + DEF + ABCDF
B + ACE + CDF + ABDEF
C + ABE + BDF + ACDEF
D + AEF + BCF + ABCDE
E + ABC + ADF + BCDEF
F + ADE + BCD + ABCEF
AB + CE + ACDF + BDEF
AC + BE + ABDF + CDEF
AD + EF + ABCF + BCDE
AE + BC + DF + ABCDEF
AF + DE + ABCD + BCEF
BD + CF + ABEF + ACDE
BF + CD + ABDE + ACEF
ABD + ACF + BEF + CDE
ABF + ACD + BDE + CEF